DEFINITIONS, ELEMENTARY APPROACH
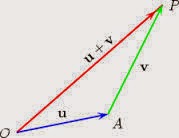
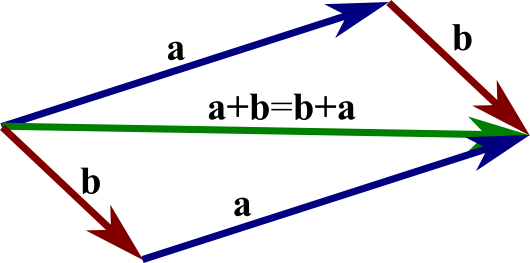
In science and engineering we frequently encounter quantities that have magnitude andmagnitude only: mass, time, and temperature. These we label scalar quantities, which remainthe same no matter what coordinates we use. In contrast, many interesting physicalquantities have magnitude and, in addition, an associated direction. This second groupincludes displacement, velocity, acceleration, force, momentum, and angular momentum.Quantities with magnitude and direction are labeled vector quantities. Usually, in elementarytreatments, a vector is defined as a quantity having magnitude and direction. To distinguishvectors from scalars, we identify vector quantities with boldface type, that is, V.Our vector may be conveniently represented by an arrow, with length proportional to themagnitude. The direction of the arrow gives the direction of the vector, the positive senseof direction being indicated by the point. In this representation, vector additionC = A +B (1.1)consists in placing the rear end of vector B at the point of vector A. Vector C is thenrepresented by an arrow drawn from the rear of A to the point of B. This procedure, thetriangle law of addition, assigns meaning to Eq. (1.1) and is illustrated in Fig. 1.1. Bycompleting the parallelogram, we see thatC = A+B = B+A, (1.2)as shown in Fig. 1.2. In words, vector addition is commutative.For the sum of three vectorsD = A+B+C,Fig. 1.3, we may first add A and B:A+B = E.
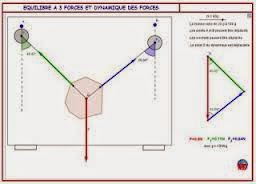
Then this sum is added to C:D = E+C.Similarly, we may first add B and C:B+C = F.ThenD = A+F.In terms of the original expression,(A +B)+C = A +(B+ C).Vector addition is associative.A direct physical example of the parallelogram addition law is provided by a weightsuspended by two cords. If the junction point (O in Fig. 1.4) is in equilibrium, the vector
sum of the two forces F1 and F2 must just cancel the downward force of gravity, F3. Herethe parallelogram addition law is subject to immediate experimental verification.1Subtraction may be handled by defining the negative of a vector as a vector of the samemagnitude but with reversed direction. ThenA− B = A+ (−B).In Fig. 1.3,A = E− B.Note that the vectors are treated as geometrical objects that are independent of any coordinatesystem. This concept of independence of a preferred coordinate system is developedin detail in the next section.The representation of vector A by an arrow suggests a second possibility. Arrow A(Fig. 1.5), starting from the origin,2 terminates at the point (Ax,Ay,Az). Thus, if we agreethat the vector is to start at the origin, the positive end may be specified by giving theCartesian coordinates (Ax,Ay,Az) of the arrowhead.Although A could have represented any vector quantity (momentum, electric field, etc.),one particularly important vector quantity, the displacement from the origin to the point1Strictly speaking, the parallelogram addition was introduced as a definition. Experiments show that if we assume that theforces are vector quantities and we combine them by parallelogram addition, the equilibrium condition of zero resultant force issatisfied.2We could start from any point in our Cartesian reference frame; we choose the origin for simplicity. This freedom of shiftingthe origin of the coordinate system without affecting the geometry is called translation invariance.
(x, y, z), is denoted by the special symbol r. We then have a choice of referring to the displacementas either the vector r or the collection (x, y, z), the coordinates of its endpoint:r↔(x, y, z). (1.3)Using r for the magnitude of vector r, we find that Fig. 1.5 shows that the endpoint coordinatesand the magnitude are related byx = r cos α, y = r cos β, z = r cos γ. (1.4)Here cosα, cosβ, and cos γ are called the direction cosines, α being the angle between thegiven vector and the positive x-axis, and so on. One further bit of vocabulary: The quantitiesAx,Ay , and Az are known as the (Cartesian) components of A or the projectionsof A, with cos2 α +cos2 β + cos2 γ = 1.Thus, any vector A may be resolved into its components (or projected onto the coordinateaxes) to yield Ax = Acosα, etc., as in Eq. (1.4). We may choose to refer to the vectoras a single quantity A or to its components (Ax,Ay,Az). Note that the subscript x in Axdenotes the x component and not a dependence on the variable x. The choice betweenusing A or its components (Ax,Ay,Az) is essentially a choice between a geometric andan algebraic representation. Use either representation at your convenience. The geometric“arrow in space” may aid in visualization. The algebraic set of components is usually moresuitable for precise numerical or algebraic calculations.Vectors enter physics in two distinct forms. (1) Vector A may represent a single forceacting at a single point. The force of gravity acting at the center of gravity illustrates thisform. (2) Vector A may be defined over some extended region; that is, A and its componentsmay be functions of position: Ax = Ax(x, y, z), and so on. Examples of this sortinclude the velocity of a fluid varying from point to point over a given volume and electricand magnetic fields. These two cases may be distinguished by referring to the vector definedover a region as a vector field. The concept of the vector defined over a region and
being a function of position will become extremely important when we differentiate andintegrate vectors.At this stage it is convenient to introduce unit vectors along each of the coordinate axes.Let ˆx be a vector of unit magnitude pointing in the positive x-direction, ˆy, a vector of unitmagnitude in the positive y-direction, and ˆz a vector of unit magnitude in the positive zdirection.Then ˆxAx is a vector with magnitude equal to |Ax | and in the x-direction. Byvector addition,A = ˆxAx + ˆyAy + ˆzAz. (1.5)Note that if A vanishes, all of its components must vanish individually; that is, ifA = 0, then Ax = Ay = Az = 0.This means that these unit vectors serve as a basis, or complete set of vectors, in the threedimensionalEuclidean space in terms of which any vector can be expanded. Thus, Eq. (1.5)is an assertion that the three unit vectors ˆx, ˆy, and ˆz span our real three-dimensional space:Any vector may be written as a linear combination of ˆx, ˆy, and ˆz. Since ˆx, ˆy, and ˆz arelinearly independent (no one is a linear combination of the other two), they form a basisfor the real three-dimensional Euclidean space. Finally, by the Pythagorean theorem, themagnitude of vector A is|A| = A2x+A2y + A2z 1/2. (1.6)Note that the coordinate unit vectors are not the only complete set, or basis. This resolutionof a vector into its components can be carried out in a variety of coordinate systems, asshown in Chapter 2. Here we restrict ourselves to Cartesian coordinates, where the unitvectors have the coordinates ˆx = (1, 0, 0), ˆy = (0, 1, 0) and ˆz = (0, 0, 1) and are all constantin length and direction, properties characteristic of Cartesian coordinates.As a replacement of the graphical technique, addition and subtraction of vectors maynow be carried out in terms of their components. For A = ˆxAx + ˆyAy + ˆzAz and B =ˆxBx + ˆyBy + ˆzBz,A±B = ˆx(Ax ±Bx )+ ˆy(Ay ± By )+ ˆz(Az ±Bz). (1.7)It shouldNote that the coordinate unit vectors are not the only complete set, or basis. This resolutionof a vector into its components can be carried out in a variety of coordinate systems, asshown in Chapter 2. Here we restrict ourselves to Cartesian coordinates, where the unitvectors have the coordinates ˆx = (1, 0, 0), ˆy = (0, 1, 0) and ˆz = (0, 0, 1) and are all constantin length and direction, properties characteristic of Cartesian coordinates.As a replacement of the graphical technique, addition and subtraction of vectors maynow be carried out in terms of their components. For A = ˆxAx + ˆyAy + ˆzAz and B =ˆxBx + ˆyBy + ˆzBz,A±B = ˆx(Ax ±Bx )+ ˆy(Ay ± By )+ ˆz(Az ±Bz). (1.7)It should be emphasized here that the unit vectors ˆx, ˆy, and ˆz are used for convenience.They are not essential; we can describe vectors and use them entirely in terms of theircomponents: A ↔ (Ax,Ay,Az). This is the approach of the two more powerful, moresophisticated definitions of vector to be discussed in the next section. However, ˆx, ˆy, andˆz emphasize the direction.So far we have defined the operations of addition and subtraction of vectors. In the nextsections, three varieties of multiplication will be defined on the basis of their applicability:a scalar, or inner, product, a vector product peculiar to three-dimensional space, and adirect, or outer, product yielding a second-rank tensor. Division by a vector is not defined.
If You Read above theory then you must solve these QUSTION to improve your skills in mathematics
Exercises
1.1.1 Show how to find A and B, given A+B and A −B.
1.1.2 The vector A whose magnitude is 1.732 units makes equal angles with the coordinate
axes. Find Ax,Ay , and Az.
1.1.3 Calculate the components of a unit vector that lies in the xy-plane and makes equal
angles with the positive directions of the x- and y-axes.
1.1.4 The velocity of sailboat A relative to sailboat B, vrel, is defined by the equation vrel = vA − vB, where vA is the velocity of A and vB is the velocity of B. Determine the
velocity of A relative to B if
vA = 30 km/hr east
vB = 40 km/hr north.
ANS. vrel = 50 km/hr, 53.1◦ south of east.
1.1.5 A sailboat sails for 1 hr at 4 km/hr (relative to the water) on a steady compass heading
of 40◦ east of north. The sailboat is simultaneously carried along by a current. At the
end of the hour the boat is 6.12 km from its starting point. The line from its starting point
to its location lies 60◦ east of north. Find the x (easterly) and y (northerly) components
of the water’s velocity.
ANS. veast = 2.73 km/hr, vnorth ≈ 0 km/hr.
1.1.6 A vector equation can be reduced to the form A = B. From this show that the one vector
equation is equivalent to three scalar equations. Assuming the validity of Newton’s
second law, F = ma, as a vector equation, this means that ax depends only on Fx and
is independent of Fy and Fz.
1.1.7 The vertices A,B, and C of a triangle are given by the points (−1, 0, 2), (0, 1, 0), and
(1,−1, 0), respectively. Find point D so that the figure ABCD forms a plane parallelogram.
ANS. (0,−2, 2) or (2, 0,−2).
1.1.8 A triangle is defined by the vertices of three vectors A,B and C that extend from the
origin. In terms of A,B, and C show that the vector sum of the successive sides of the
triangle (AB +BC +CA) is zero, where the side AB is from A to B, etc.
1.1.9 A sphere of radius a is centered at a point r1.
(a) Write out the algebraic equation for the sphere.
(b) Write out a vector equation for the sphere.
ANS. (a) (x −x1)2 +(y −y1)2 + (z −z1)2 = a2.
(b) r = r1 +a, with r1 = center.
(a takes on all directions but has a fixed magnitude a.)
1.2 Rotation of the Coordinate Axes 7
1.1.10 A corner reflector is formed by three mutually perpendicular reflecting surfaces. Show
that a ray of light incident upon the corner reflector (striking all three surfaces) is reflected
back along a line parallel to the line of incidence.
Hint. Consider the effect of a reflection on the components of a vector describing the
direction of the light ray.
1.1.11 Hubble’s law. Hubble found that distant galaxies are receding with a velocity proportional
to their distance from where we are on Earth. For the ith galaxy,
vi = H0ri ,
with us at the origin. Show that this recession of the galaxies from us does not imply
that we are at the center of the universe. Specifically, take the galaxy at r1 as a new
origin and show that Hubble’s law is still obeyed.
1.1.12 Find the diagonal vectors of a unit cube with one corner at the origin and its three sides
lying along Cartesian coordinates axes. Show that there are four diagonals with length √3. Representing these as vectors, what are their components? Show that the diagonals
of the cube’s faces have length √2 and determine their components.
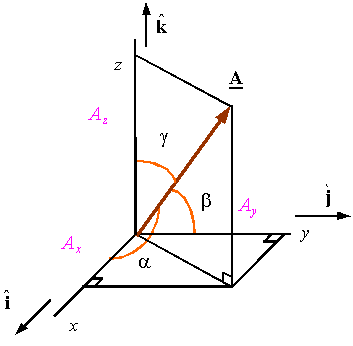



No comments:
Post a Comment